Cambridge AS Level (9709) Pure Mathematics 1
Instructor
beyondcountables.com
36
Students
enrolled
- Description
- Curriculum

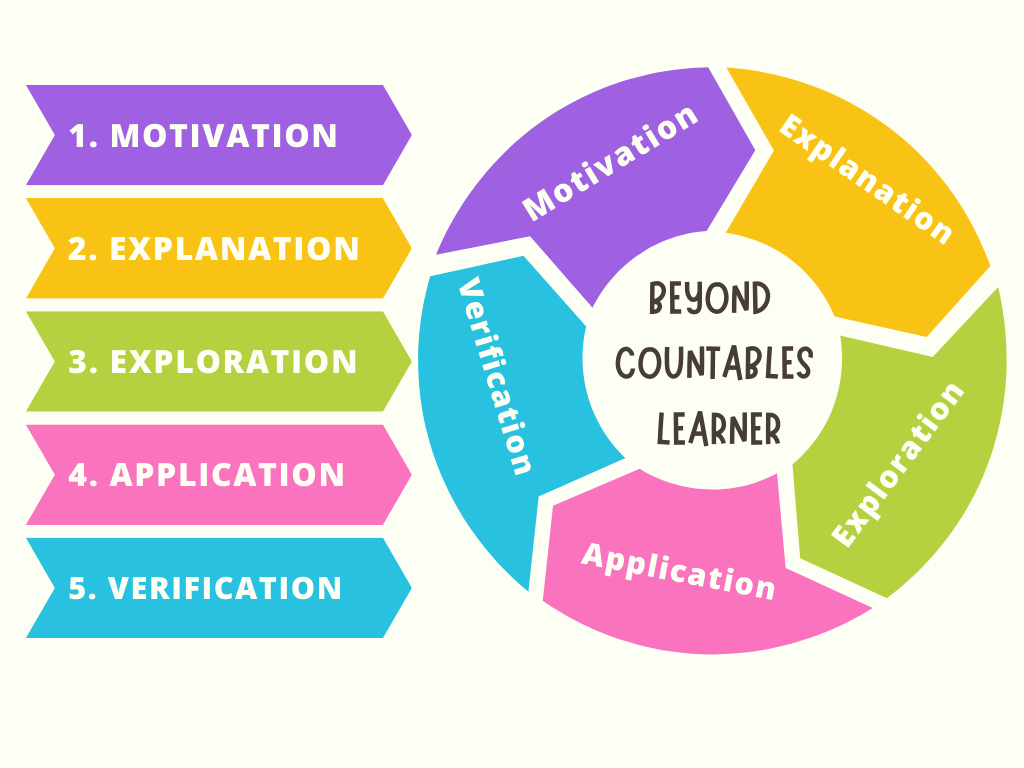
Our Approach to Teaching and Learning:
We follow the 5-step process depicted in the picture below.
AS Level Pure Mathematics Paper 1 content is covered under eight topics.
-
1Quadratics
- Forms of quadratics - Completing the square, Vertex form and Standard form
- Classifying the nature of roots using discriminant
- Solving quadratic equations and inequalities
- Solving simultaneous equations involving quadratics
- Reduction of higher degree polynomials to quadratics and solve them
-
2Functions
- Domain, Range and types of functions,
- Function composition and inverse functions
- Domain restriction for the existence of inverse functions
- Graphical approach to inverse functions - reflection along the line y=x
- Transformations of functions - translation/shift, reflection and stretch/dilation
-
3Coordinate Geometry
- Equation of straight lines
- Relationship between straight lines - intersecting/non-intersecting lines, parallel lines and perpendicular lines
- Equation of a circle
- Solving equations that involve equation of a line and an equation of a circle simultaneously - algebraic and geometric approach
-
4Circular Measure
- Radian Measure - new way to measure angle
- Relationship between radian and degrees
- Arc length and area of sector in both radian and degree measures of an angle
- Area of a segment
-
5Trigonometry
- Graph of trigonometric functions
- Unit circle and multiples of exact angles 30o, 45o, 60o
- Inverse trigonometric functions and its principal values
- Trigonometric Pythagorean identities
- Solving simple trigonometric equations
-
6Series
- Binomial expansion for integer powers
- Arithmetic and geometric progressions
- General term/formula of AP and GP and related problems
- Arithmetic and geometric series with finite number of terms
- Infinite geometric series and the condition for convergence
-
7Differentiation
- Gradient of a curve at a point as limit of gradients of certain sequence of chords
- Derivative of polynomial functions
- Differentiation and its relevance in tangents and normals
- Increasing and decreasing property of curve using derivatives
- Stationary points and sketching of graphs
-
8Integration
- Reverse process of differentiation leads to the concept of integration
- Finding integrals of the form (ax+b)n
- Finding the constant of integration
- Definite integrals with simple improper integrals
- Using integration to find Area under curve and Volume of solid of revolution about axes