CBSE Mathematics Higher secondary level (Year 2)
- Description
- Curriculum
- Announcement
Assessment structure:
The assessment has two components- External and internal assessment
The external assessment is a theory paper of 80 marks and duration 3 hours.
Internal assessment is of 20 marks.
Question paper design:
Grade 12 CBSE course content is covered under the following six topics.
-
1
Relations and Functions- Types of relations: reflexive, symmetric, transitive and equivalence relations.
- One to one and onto functions
- Definition of Inverse Trigonometric Functions
- Range, domain, principal value branch.
- Graphs of inverse trigonometric functions.
-
2
Algebra
- Matrices
- Types of matrices
- Transpose of a matrix
- Symmetric and skew symmetric matrices
- Operations on matrices
- Invertible matrices and proof of the uniqueness of inverse
- Determinants
- Determinant of a square matrix (up to 3 x 3 matrices)
- Minors, co-factors
- Applications of determinants in finding the area of a triangle.
- Adjoint and inverse of a square matrix.
- Consistency, inconsistency and number of solutions of system of linear equations by examples
- Solving system of linear equations in two or three variables using inverse of a matrix
-
3
Calculus
- Continuity and Differentiability
- Chain rule
- Derivative of inverse trigonometric function
- Derivative of implicit functions.
- Concept of exponential and logarithmic functions.
- Derivatives of logarithmic and exponential functions.
- Logarithmic differentiation,
- Derivative of functions expressed in parametric forms.
- Second order derivatives.
- Applications of Derivatives
- Rate of change of quantities, increasing/decreasing functions, maxima and minima
- Integrals
- Integration as inverse process of differentiation.
- Integration of a variety of functions by substitution, by partial fractions and by parts,
- Fundamental Theorem of Calculus (without proof).
- Basic properties of definite integrals and evaluation of definite integrals.
- Applications of the Integrals -Applications in finding the area under simple curves,
- Differential Equations Definition, order and degree, general and particular solutions of a differential equation.
- Solution of differential equations
- Solutions of linear differential equation
-
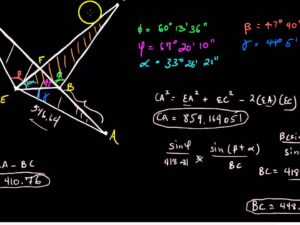
4
Vectors and Three-Dimensional Geometry
- Vectors and scalars, magnitude and direction of a vector.
- Direction cosines and direction ratios of a vector.
- Types of vectors
- Position vector of a point, negative of a vector,
- Components of a vector,
- Addition of vectors, multiplication of a vector by a scalar,
- Position vector of a point dividing a line segment in a given ratio.
- Definition, Geometrical Interpretation of scalar dot product
- Properties and application of scalar (dot) product of vectors,
- Vector (cross) product of vectors
- Three - dimensional Geometry
- Direction cosines and direction ratios of a line joining two points.
- Cartesian equation and vector equation of a line,
- Skew lines, shortest distance between two lines.
- Angle between two lines.
-
5
Linear Programming
- Linear Programming-Introduction, related terminology
- Graphical method of solution for problems in two variables,
- Feasible and infeasible regions (bounded or unbounded),
- Feasible and infeasible solutions,
- Optimal feasible solutions (up to three non-trivial constraints).
-
6
Probability
- Conditional probability,
- Multiplication theorem on probability,
- Independent events,
- Total probability,
- Bayes’ theorem,
- Random variable and its probability distribution,
- Mean of random variable
Assessment Structure
All students should take 2 components which will be assessed externally.students who have chosen core syllabus will take paper 1 and 3. And students who have chosen extended syllabus will take paper 2 and 4.
Our Approach to Teaching and Learning:
We follow the 5 step process depicted in the picture below.
-
Motivation
-
Explanation
-
Exploration
-
Application
-
Verification
