IGCSE Additional Mathematics (0606)
Instructor
beyondcountables.com
37
Students
enrolled
- Description
- Curriculum

Course description
Cambridge IGCSE Mathematics motivates learners to improve their mathematical abilities, viewing them as essential life skills and a strong basis for further studies in mathematics or to support skills in other subjects. It enhances students’ proficiency, confidence, and skill in applying methods with or without the aid of a graphic display calculator.It cultivates learners’ abilities in mathematical inquiry and/or modeling, promoting both conceptual understanding and proficiency in applying techniques and methods.
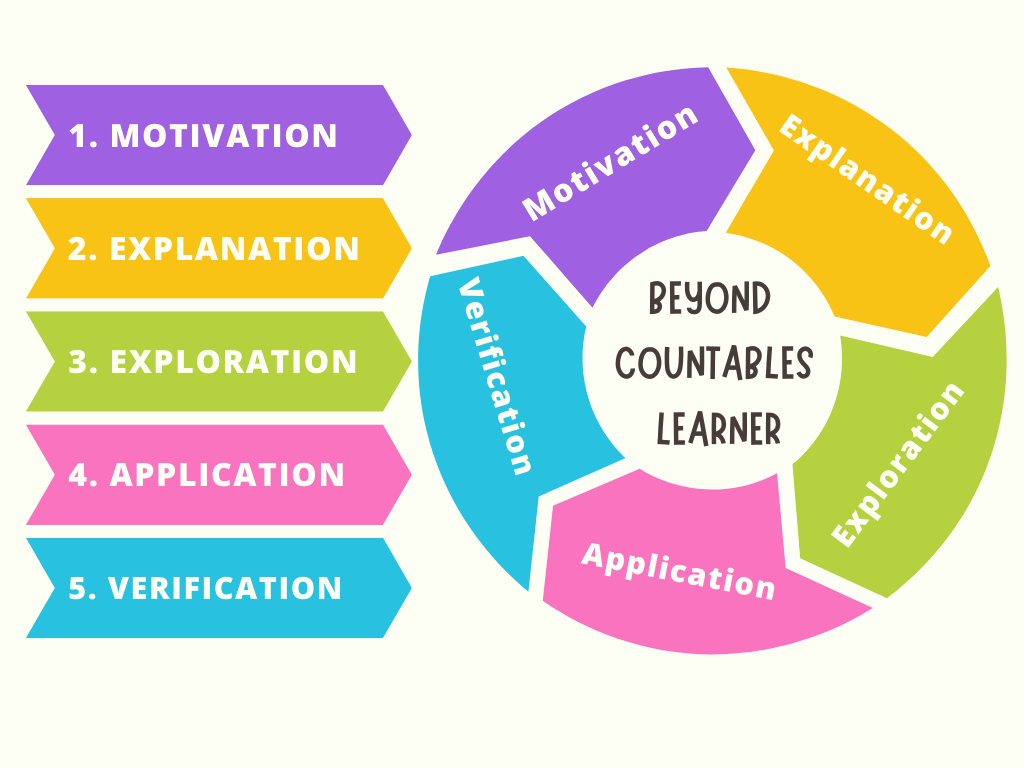
Our Approach to Teaching and Learning:
We follow the 5-step process depicted in the picture below.
The following topics are covered in this course
-
1Functions
- Functions, domains and range
- Use of function notation
- Modulus of a function
- Inverse functions
- Composite functions
- Sketching graphs of a functions and its inverse
-
2Quadratic function
- Finding the Maximum and minimum values of quadratic function
- Sketching graphs for quadratic functions
- Intersection of line and the curve
- Finding solutions for quadratic inequalities
-
3Factors of polynomials
- Remainder and factor theorem
- Finding factors of polynomials
- Solving cubic equations
-
4Equations, inequalities and graphs
- Solving modulus equations using algebraic or graphical methods
- Solving modulus inequalities using algebraic or graphical methods
- Using substitution to solve quadratic equations
- Sketching graphs of cubic polynomials and their moduli
- Graphical solution for cubic inequalities
-
5Simultaneous equations
- Elimination method
- Substitution method
-
6Logarithmic and exponential functions
- Properties and graphs of logarithmic and exponential functions
- Usage of Laws of logarithms
- Change of base of logarithms
- Solving simple exponential equations
-
7Straight-line graphs
- Equation of a straight line
- Condition for lines to be parallel and perpendicular
- Finding midpoint, length of a line and perpendicular bisector
- Transforming relationships to straight line form
- Calculating gradient or intercepts of the transformed graphs
-
8Coordinate geometry of the circle
- Identifying the center and radius of the circle from its equation
- Intersection of a circle and a straight line
- Finding equations of tangent
- Intersection of two circles
-
9Circular measure
- Arc length and area of sector of a circle
- Radians measure
-
10Trigonometry
- Trigonometric functions for angles of any size
- Graphs of trigonometric functions
- Transformations of trigonometric graphs
- Trigonometric identities
-
11Permutations and combinations
- Identifying the difference between permutations and combinations
- Usage of the notation n!
- simple problems on arrangement and selection.
-
12Series
- The binomial theorem
- The formula for a binomial coefficient
- The expansion of (1 + x)n
- Identifying arithmetic and geometric progression
- Difference between arithmetic and geometric progression
- The sum of the terms of an arithmetic or geometric progression
- The condition for the convergence of a geometric progression,
-
13Vectors in two dimensions
- Vector notation
- Zero and unit vectors
- Magnitude of a vector
- Addition and subtraction of vectors
- Multiplying a vector by a scalar
- compose and resolve velocities.
-
14Calculus
- Limits
- Rules of differentiation
- Finding stationary points
- Practical problems involving Maximum and minimum points
- Using second derivatives
- Finding equations of tangents and normals
- Derivatives of standard functions
- Understanding integration
- Integrate sums of terms in powers of x